疑問の出どころ
通常はカメラのファインダーやモニタで確認しながら撮影をするため、タイトルのような疑問は出ないかと思います。
ところが、ステレオカメラ、structure from motion、SLAM(自己位置推定)、ARなどの分野では撮られた写真(画像)から位置関係を割り出す計算が必要な為に基礎技術となっています。
そこでこの記事では基礎技術を理解するために、撮影した物体のある点(X,Y,Z)が画像の縦横何ピクセル目の点なのか?についてカメラの内部パラメータを使って計算していきたいと思います。
考えている状況
カメラの位置を固定して動くサッカーボールを撮影する場合、サッカーボールが動いた分だけ画像内のボールも動きます。
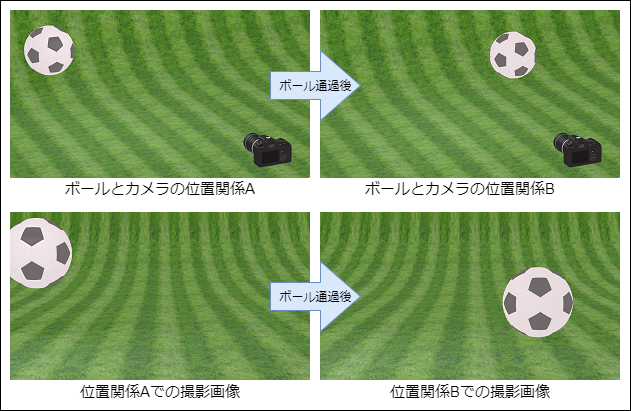
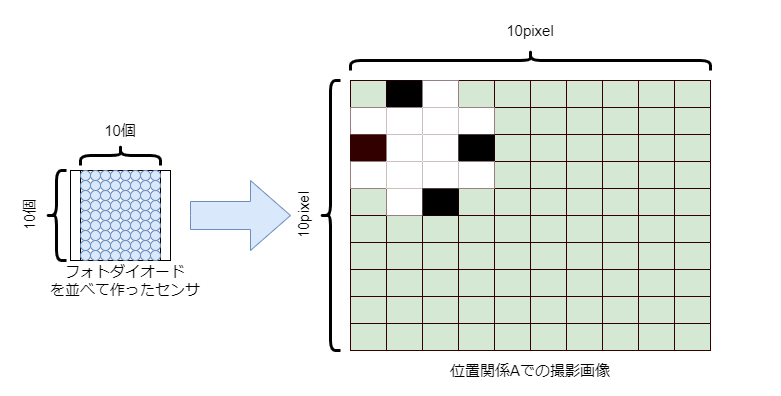
これは単純化して考えると、ボールの位置変化に応じてカメラのセンサ(フォトダイオード/CMOSセンサ)の反応する部分が移動していく為です。
この記事の最終ゴールはサッカーボールがある位置(X,Y,Z)にあるとき、画像では縦横それぞれ何pixel目に表示されるのか?です。
図のボールとカメラの位置関係Aで撮影したボールを例に考えていきます。
状況の単純化とピンホールカメラモデル
以下では話を単純にするためカメラのセンサーは$10 \times 10$のフォトダイオードを並べたものとして考えます。
(フォトダイオード1個につき1ピクセル描画するものとします。)
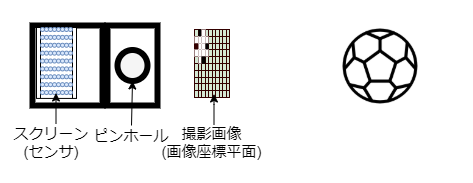
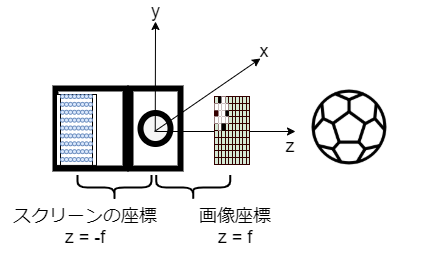
ピンホールカメラモデルでは、原点はピンホール部分でセンサ(ピンホールカメラでは感光体を塗ったスクリーン)の位置は画像と同じ位置です。
センサ(スクリーン)上では上下反転した映像が映るため、画像の位置(画像座標平面と呼ぶ)は人が見るときの位置と同じ所で考えます。(透視投影カメラモデル)
こうすると原点と画像と撮影対象が順番に並ぶので、マイナスの奥行き方向を考えずに済みます。
最後に焦点距離をfとすると、それぞれの位置関係は最終的に下図のようになります。
ピンホールカメラとレンズカメラの違いはthothchildrenさんの解説記事が分かりやすいです。(ピンホールとレンズの違いを知りたい)
3次元座標から2次元座標へ
上で考えた透視投影カメラモデルを元に、画像上の点(x,y,z)とサッカーボールのとある点の座標(X,Y,Z)の対応を考えます。
画像に写っているのであればz座標(奥行き)はピクセルの位置に関わらず全てfです。
つまり、画像の点(x,y,z) は(x,y,f)です。
次にy座標(高さ)を考えます。
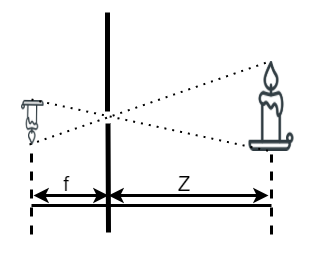
焦点距離よりも遠い位置での倍率計算をするとピンホールカメラでは $ \frac{f}{Z} = \frac{y}{Y}$ が成り立ちます。
成り立つ理由は下図のように三角形の相似関係から f:Z = y:Yとおけるためです。
x座標(幅)についても同様に $ \frac{f}{Z} = \frac{x}{X}$ が成り立つので、結果的に画像上の点(x,y,z)は($f\times \frac{X}{Z}$, $f\times \frac{Y}{Z}$, $f$)となります。
画像上の点は2次元なのでzを無視して、 (x,y) = ($f\times \frac{X}{Z}$, $f\times \frac{Y}{Z}$)となります。
*1:何ピクセル目なのか?にはまだ応えられませんが、一応ここまでで撮影物体が写るスクリーン(画像)の位置の答えです。
*2:fで正規化したもの(正規化画像座標系)を考えると(x,y,z) = ($\frac{X}{Z}$, $\frac{Y}{Z}$, 1)となります。
カメラの内部パラメータについて
これまで画像の中心を原点として考えてきましたが、通常は画像の左上を原点として考えるためオフセットを行います。
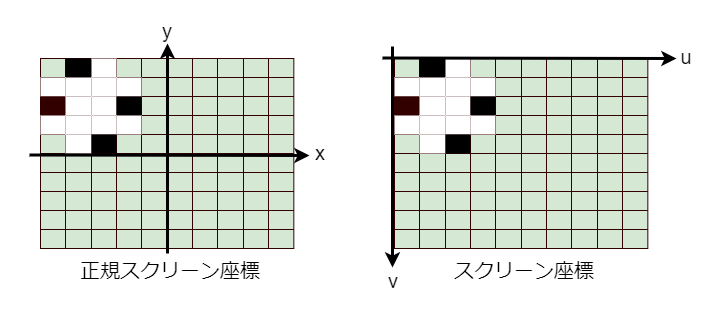
このときx軸方向のオフセット量を$C_x$ y軸方向のオフセット量を$C_y$として軸の名前をそれぞれu,vとすると
u = $f\times \frac{X}{Z} + C_x$
v = $f\times \frac{Y}{Z} + C_y$
となります。これを行列で表すと
$ \left[\begin{array}{ccc} u \\ v \\ 1 \end{array}\right]= \left[\begin{array}{ccc} f & 0 & C_x \\ 0 & f & C_y \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc} \frac{X}{Z} \\ \frac{Y}{Z} \\ 1 \end{array}\right]$
となります。
ボールのとある点の位置Zは画像データからでは分からないので、画像の位置からサッカーボールの位置を考えている人にとって扱いやすいように
$\left[\begin{array}{ccc} \frac{X}{Z} \\ \frac{Y}{Z} \\ 1 \end{array}\right]$から$\frac{1}{Z}$をくくって、sとおいた
$ s \left[\begin{array}{ccc} u \\ v \\ 1 \end{array}\right]= \left[\begin{array}{ccc} f & 0 & C_x \\ 0 & f & C_y \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc} X \\ Y \\ 1 \end{array}\right]$
の形の式が代表的です。
$\left[\begin{array}{ccc} f & 0 & C_x \\ 0 & f & C_y \\ 0 & 0 & 1 \end{array}\right]$の部分をカメラの内部パラメータと呼びます。
焦点距離が$f_x$と$f_y$になっている理由:https://mem-archive.com/2018/02/25/post-201/
結局、撮影した物体は画像のどこに写るのか?
ここまでで算出したuとvが最初の疑問の答えですが、これはアナログのピンホールカメラを考えている為にuもvも整数である必要が無いです。
デジタルデータでは画像内の位置=ピクセルの数なので、uもvも整数化する必要が出てきます。
これに伴って焦点距離fについてもmmではなくピクセル単位で表す必要があります。
焦点距離fのピクセル距離は画像の解像度とセンサの物理幅の関係から
f[mm] : f[pixel] = w[センサーの物理的な幅mm] : W[画像の解像度]
f[pixel] = f[mm]$ \times \frac{W[画像の解像度]}{w[センサーの幅mm]} $
が成り立ちます。
上の式はセンサの幅と画像の解像度(横方向)について考えていますが、当然、縦方向も同様に計算出来るので便宜的に$f_x$[pixel]と$f_y$[pixel]としてuとvの式に焦点距離を代入すると下のような式になります。
u = $f_x [pixel] \times \frac{X}{Z} + C_x$
v = $f_y [pixel] \times \frac{Y}{Z} + C_y$
この式から算出したuとvをそれぞれ量子化(例:小数第一位で四捨五入)した値がすなわち撮影した物体が映っているピクセルの位置になります。
(実際のカメラの焦点距離について:https://fotootaku.com/what-is-focal-length/)
注1 : ピンホールカメラと凸レンズカメラの倍率の違い
実際はピンホールカメラではなく、レンズで撮影するケースがほとんどだと思います。
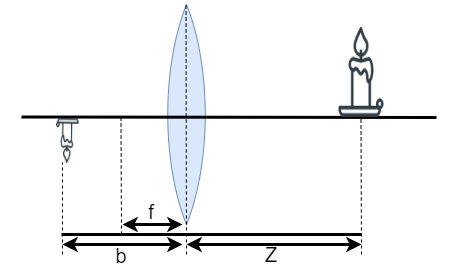
凸レンズの倍率は焦点距離よりも遠くに撮影物体を置いた場合にはピンホールカメラと違い
$ \frac{b}{a} = \frac{f}{(a-f)}となります。
ここで焦点距離fは数cm程度なのに対してレンズと撮影物体の距離Zはそれよりも大きい場合が殆どである為、$\frac{b}{a} = \frac{f}{(a-f)} ≒ \frac{f}{(a)}$と近似が出来ます。
注2:スケールが分からないとは?
画像だけではカメラの近くの物体なのか遠くの物体なのか本当は不明ですが、人は遠近感を感じることが出来ます。
その為、人の感覚を騙した写真などが撮れたりします。これは画像からではスケール(大きさ)が分からな例です。