3Dデータから体積を出す方法として、原点と面で作られる三角錐を足し合わせるというのが有名です。
例としてドーナッツ(円環体)の体積をobjファイルを読み込んでpythonを使って出してみたいと思います。
スクリプトだけ欲しい方はこちら(https://github.com/samsumario/el_oso_ve_efectos/tree/main/obj_volume)
3Dモデルの用意
Free3Dで公開されているモデルを使用しました:https://free3d.com/3d-model/doughnut-462509.html
わざわざダウンロードしたのは最初からblenderで円環体を作ろうとして挫折した為です。。。

ファイルをblenderで開いて、円環体のTorusオブジェクト以外は全部装飾なので削除して強引にひん剝きます。
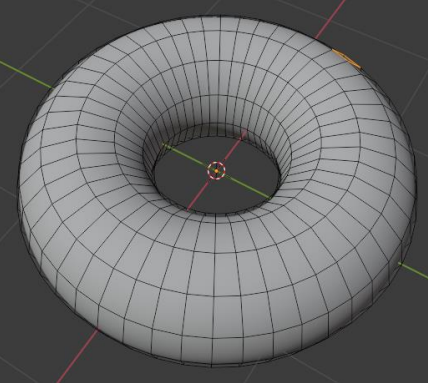
三角錐を作って体積を出そうとしているのに、ダウンロードモデルは見ての通り四角メッシュです。
これは、三角メッシュよりも四角メッシュの方がカーブを綺麗に出せる為で、有機的なモデルを作る場合に選択されることが多いです。
今回はblenderのエディットモードで三角メッシュに変換しました。

最後にpythonで扱いやすく(?)する為にobjファイルで出力します。
出力するときはオプションのGeometryで「Apply Modifiers」をoffに、「Triangle Faces」をonにして出力しています。
これでようやくシンプルな円環体のポリゴンモデルの完成です。
objファイルについて
今回は三角メッシュで保存しているので、objファイルのポリゴンデータは”f”キーワードで3つの頂点番号が書かれています。
objファイルの詳細は「YTMMWORK」さんの記事が分かりやすかったです。
三角錐の体積計算
三角錐の体積を計算する方法ですが答えとしては下記です。
\( \frac{1}{6} ( \vec{a} \times \vec{b} ) \cdot \vec{c} \)
初めて見た時に意味が分からなかったので、下記は一応説明を忘備録として残します。
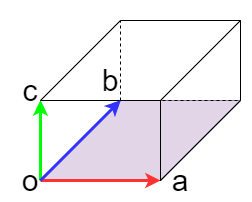
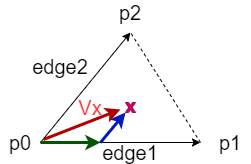
先ずは外積 \( \vec{a} \times \vec{b} \)の部分は 図の紫部分を指していて、ベクトルaとベクトルbのなす面積となります。
直方体の場合は底面積 \( \vec{a} \times \vec{b} \) に高さ\( |\vec{c}| \)をかけると体積となります。
ではベクトルcが傾いていた場合は?と言うと、高さは \( \vec{c} \times \csc \theta \)で計算出来ます。
つまり底面積×高さの公式に当てはめると内積そのままとなります。
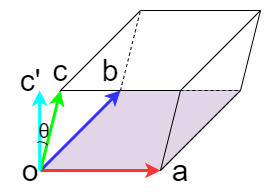
ここで、三角錐の公式 \( \frac{1}{3} \times 高さ \times 面積 \) にそれぞれ値を入れると
\( \frac{1}{3} \times \vec{c} \times \csc \theta \times \frac{1}{2} \vec{a} \times \vec{b} \)となるので、これを整理して
\( \frac{1}{6} ( \vec{a} \times \vec{b} ) \cdot \vec{c} \)
となります。(底面積が半分なので\( \frac{1}{6} \)が出てくる)
アルゴリズムについて
ポリゴンデータと三角錐の体積の計算方法の次はアルゴリズムについて解説します。
objファイルから適当に1個のポリゴンを選ぶと三角形になるので、三角形の3点に原点を足して無理やり三角錐にしてやります。
イメージ的にはドーナッツの外側の三角形を選んで穴の真ん中を原点とした場合に下図のような三角錐になります。

この状態ではドーナッツの穴の部分まで体積が足されることになるのですが、今度はドーナッツの穴の内側の三角メッシュを選ぶと丁度良く空洞部分の体積が得られます。

問題はどうやって都合よく穴の外側の三角錐から穴の内側の三角錐を引き算するか?です。
objファイルは面を表から見た時に反時計回りになるように順番に座標を決めているそうなので、その順番通りにベクトル化してやると上で求めた三角錐の体積の外積計算部分\( ( \vec{a} \times \vec{b} ) \)によって±が出てきます。
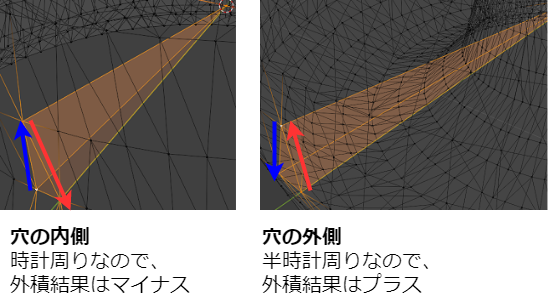
これで都合よくプラスとマイナスが打ち消しあって、ドーナッツの体積が出てきます。
pythonコードサンプル
gitにアップロードしてあるコード説明です。(https://github.com/samsumario/el_oso_ve_efectos/tree/main/obj_volume)
objファイルを読み込むdef read_obj_fileと三角錐の体積をひたすら計算して足していくdef cal_volumeの2つに分けました。
read_obj_fileの内容
ファイルを開いて、上から1行ずつテキストとして読み込んでいきます。
vから始まる行が頂点(vertex)の位置情報、fから始まる行が三角メッシュを構成する頂点情報なのでそれぞれarrayとして追加していきます。
一応、読み込み結果確認ということで、コマンドラインに頂点とメッシュの個数を表示しています。
cal_volumeの内容
頂点座標とメッシュデータを貰ったら、メッシュ1つを取り出して対応する頂点座標を引っ張ってきます。
あとはnp.linalg.det(dV)/6で体積計算をしています。
計算結果
円環体の体積の公式は穴の半径をa、一番外側の半径をbとすると下記。
\( V = \frac{1}{4} \pi^2(a + b)(a – b)^2 \)
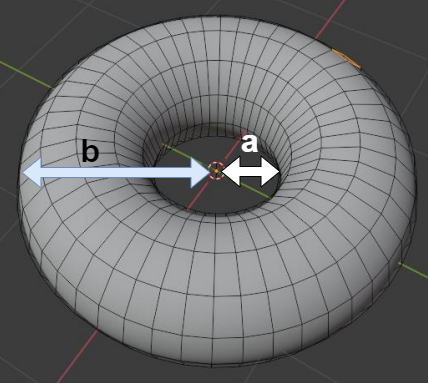
用意したモデルのblenderのunitを見るとa=0.48 , b=1.52なので体積およそ5.3です。
pythonで計算したところ、結果は5.08と少し小さめに出ました。
これは、頂点(vertex)を結んで小さな面を作ることで円を表現している為に理想形状よりしぼんでしまう為かと思われます。