前回の日記でobjファイルの読み込みをやってみたので、今回はその延長でobjファイルで読み込んだメッシュと任意の点からレイキャストした結果を取得してみます。
スクリプトだけ欲しい方はこちら(https://github.com/samsumario/el_oso_ve_efectos/tree/main/raycast)
objファイルの読み込み
ファイルの読み込みは前回の日記と同じコードで読み込みました。
メッシュと直線の交点を計算する
メッシュ上の3点(p1,p1,p2)で作られる三角形を2つのベクトルで表してみます。
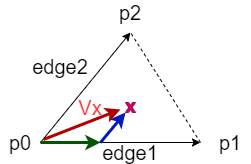
図のようにベクトルedge1(p0->p1)、ベクトルedge2(p0->p2)と置くと、三角形の中の点(赤いx)はedge1とedge2を組み合わせることで表現出来ます。
この時edge1をu倍、edge2をv倍したことにして、p0からxまでのベクトルをVxとすると下記の式になります。
\( \overrightarrow{Vx} = u \times \overrightarrow{edge1} + v \times \overrightarrow{edge2} \)
点xの座標は
\( x = p0 + u \times \overrightarrow{edge1} + v \times \overrightarrow{edge2} \)
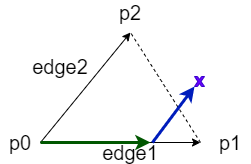
三角形の中に点がある場合はuとvの条件は下記の3つになります。
\( 0 \text{≦} u \text{≦} 1 \)
\( 0 \text{≦} v \text{≦} 1 \)
\( 0 \text{≦} u + v \text{≦} 1 \)
次にレイの式ですが、レイの出発点をRo、レイの方向Rd、距離(Rdを何倍するか?)をtとすればレイの到達地点は
\( P = Ro + t \times \overrightarrow{Rd} \)
となります。

計算したいのは、レイの到着地点が三角形の中にあるかどうか?なのでP = xつまり交点は下記の式で計算します。
\( Ro + t \times \overrightarrow{Rd} = p0 + u \times \overrightarrow{edge1} + v \times \overrightarrow{edge2} \)
式を整理して
\( u \times \overrightarrow{edge1} + v \times \overrightarrow{edge2} - t \times \overrightarrow{Rd} = Ro – p0 \)
ベクトルの部分は3次元なので、
\( u \times \left[ \begin{array}{c} x1 \\ y1 \\ z1 \\ \end{array} \right]+ v \times \left[ \begin{array}{c} x2 \\ y2 \\ z2 \\ \end{array} \right] - t \times \left[ \begin{array}{c} xr \\ yr \\ zr \\ \end{array} \right] = \left[ \begin{array}{c} xd \\ yd \\ zd \\ \end{array} \right] \)
ここでこの式を解くにはクラメルの公式を使います。三階線型方程式系(wikiリンク)というのが今回使うもの。
これでu,v,tが求まるのでメッシュと直線の交点が求まります。
メッシュと直線が交差しない場合(平行なとき)は \( \det ( \overrightarrow{edge1} , \overrightarrow{edge2}, \overrightarrow{Rd} ) \)の値が0以下になります。
[Möller97]の論文によるとこの平行判定は0の代わりに十分小さい正の数1e-6を使って判定していますので、コードではこれを真似しています。
( Möller97 : Tomas Möller, Ben Trumbore. 1997. Fast, Minimum Storage Ray/Triangle Intersection. Journal of Graphics Tools (JGT) 2, 1, 21-28)
交点の計算スクリプト
全体のスクリプト(https://github.com/samsumario/el_oso_ve_efectos/tree/main/raycast)

